Credit Scoring Development Using R - Part 2
Contents
This is the second part of a 3-parts series.
4.0 Univariate Analysis
4.1 Fine Classing
Fine classing is a technique that groups a variable’s values into a number of fine bins. Using these bins, a measure of the variable’s predictive power, known as information value (IV), can be computed. Also from these fine bins, further grouping can be carried out to result in coarse classing. As will be shown in the section below, bins from coarse classing are the bins that will be used in a credit scorecard.
Specifically, the fine classing technique used in this post is called the frequency method in the package scorecard. What this technique entails is grouping a variable’s values by having equal percentage of counts in each bin. This is a commonly used technique (see the note below). Following industry practice, the maximum number of fine bins is set at 20.
Note
-
There are other techniques available in the package
scorecard. Interested readers are referred to its
manual. -
The number of fine bins depends on the distribution of the variable. Some variables will have concentration in some values. In such cases, the number of fine bins will turn out to be less than 20.
-
The frequency method in the package
scorecardworks with numeric variables only. It is therefore necessary to convert or recode character variables (e.g. sex, education etc.) into numeric variables before hand (as the collectors of the data set used here had done).
From this point on, the package scorecard will be used.
|
|
|
|
|
|
| var | iv |
|---|---|
| limit_bal | 0.1785871 |
| sex | 0.0079849 |
| education | 0.0164957 |
| marriage | 0.0056892 |
| age | 0.0193498 |
| bill_amt1 | 0.0128997 |
| bill_amt2 | 0.0146458 |
| bill_amt3 | 0.0128501 |
| bill_amt4 | 0.0148755 |
| bill_amt5 | 0.0153958 |
| bill_amt6 | 0.0247551 |
| pay_amt1 | 0.1066663 |
| pay_amt2 | 0.0798784 |
| pay_amt3 | 0.0744712 |
| pay_amt4 | 0.0490983 |
| pay_amt5 | 0.0421035 |
| pay_amt6 | 0.0199621 |
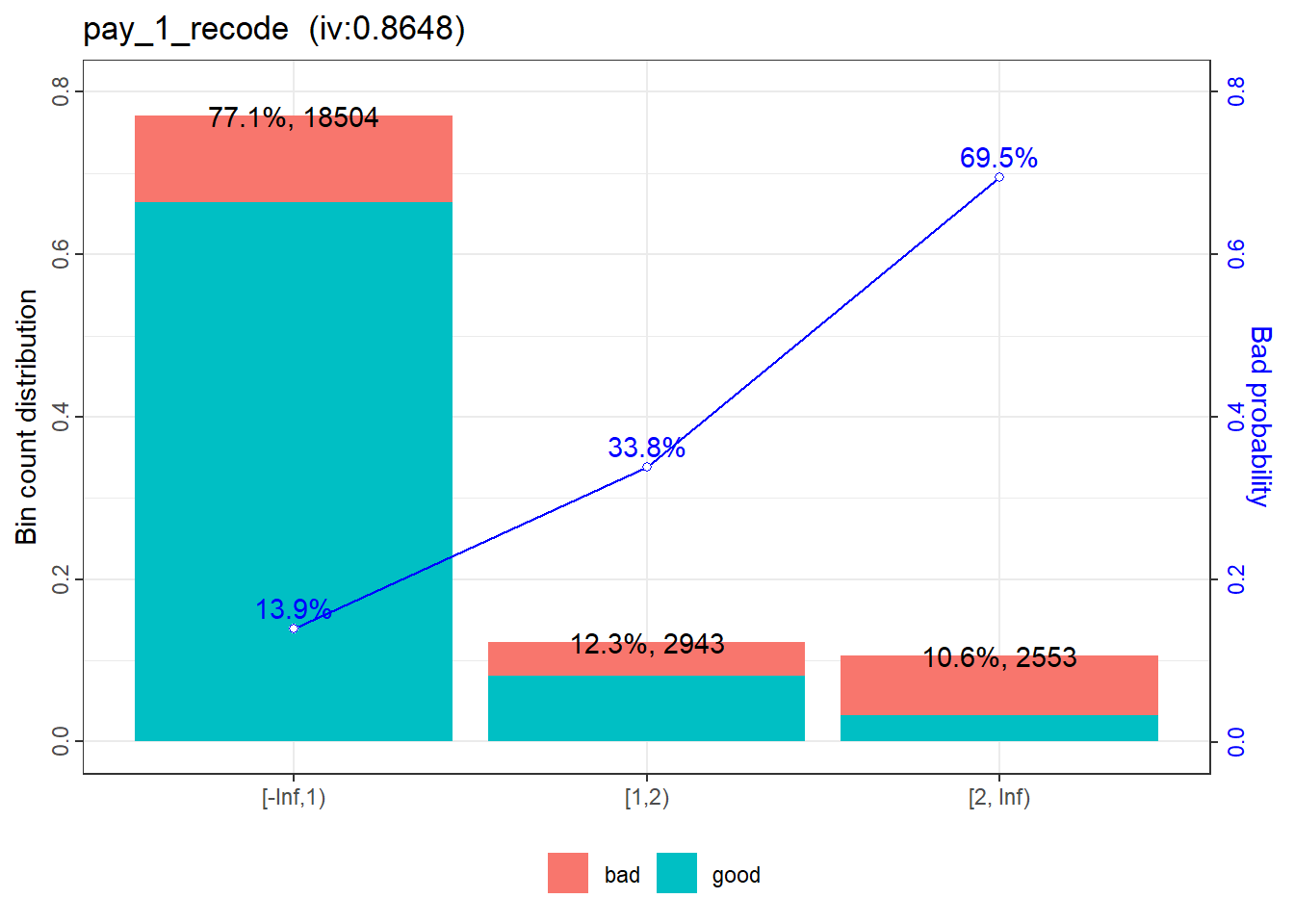
| pay_1_recode | 0.8648336 |
| pay_2_recode | 0.5459762 |
| pay_3_recode | 0.4117610 |
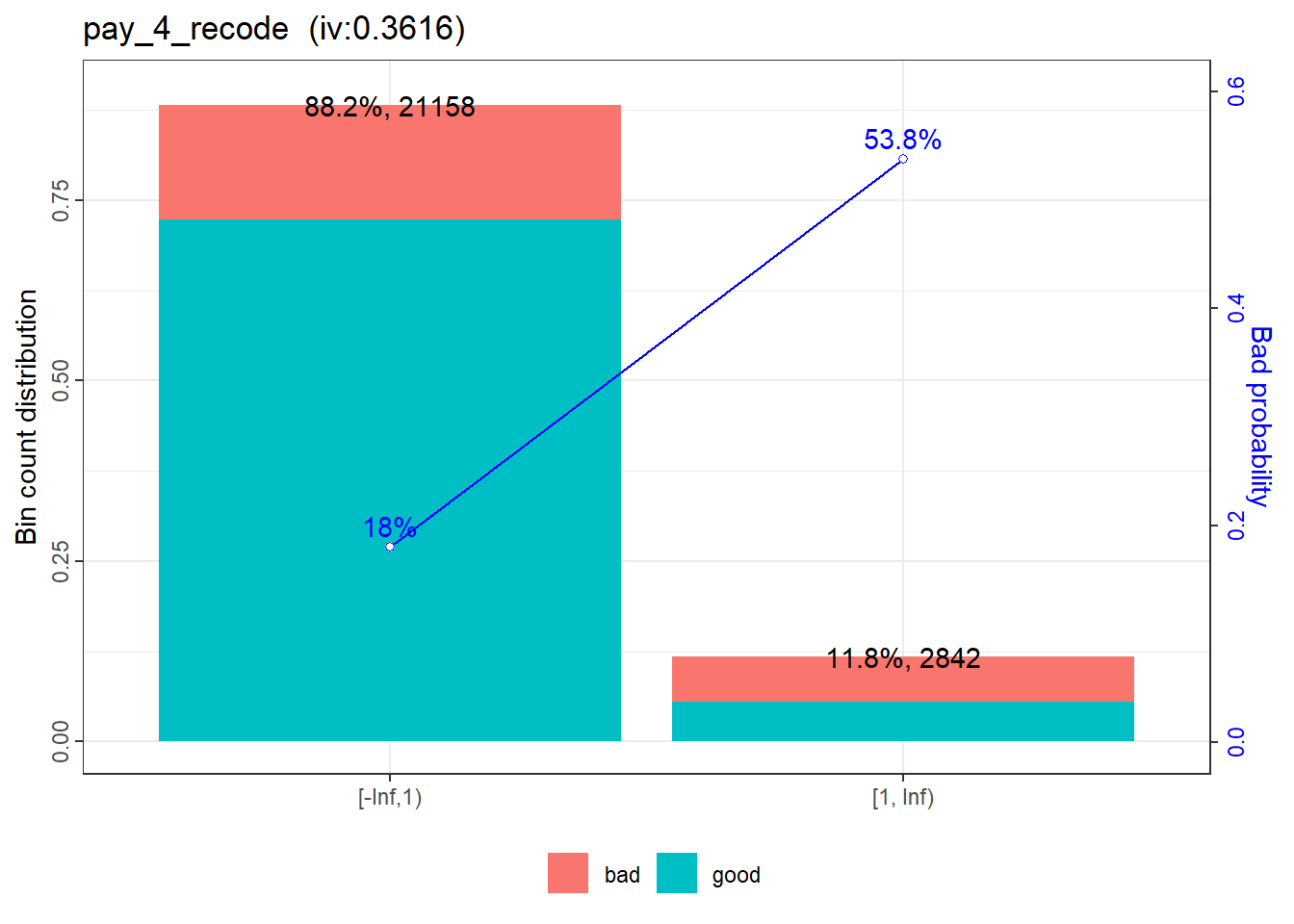
| pay_4_recode | 0.3616306 |
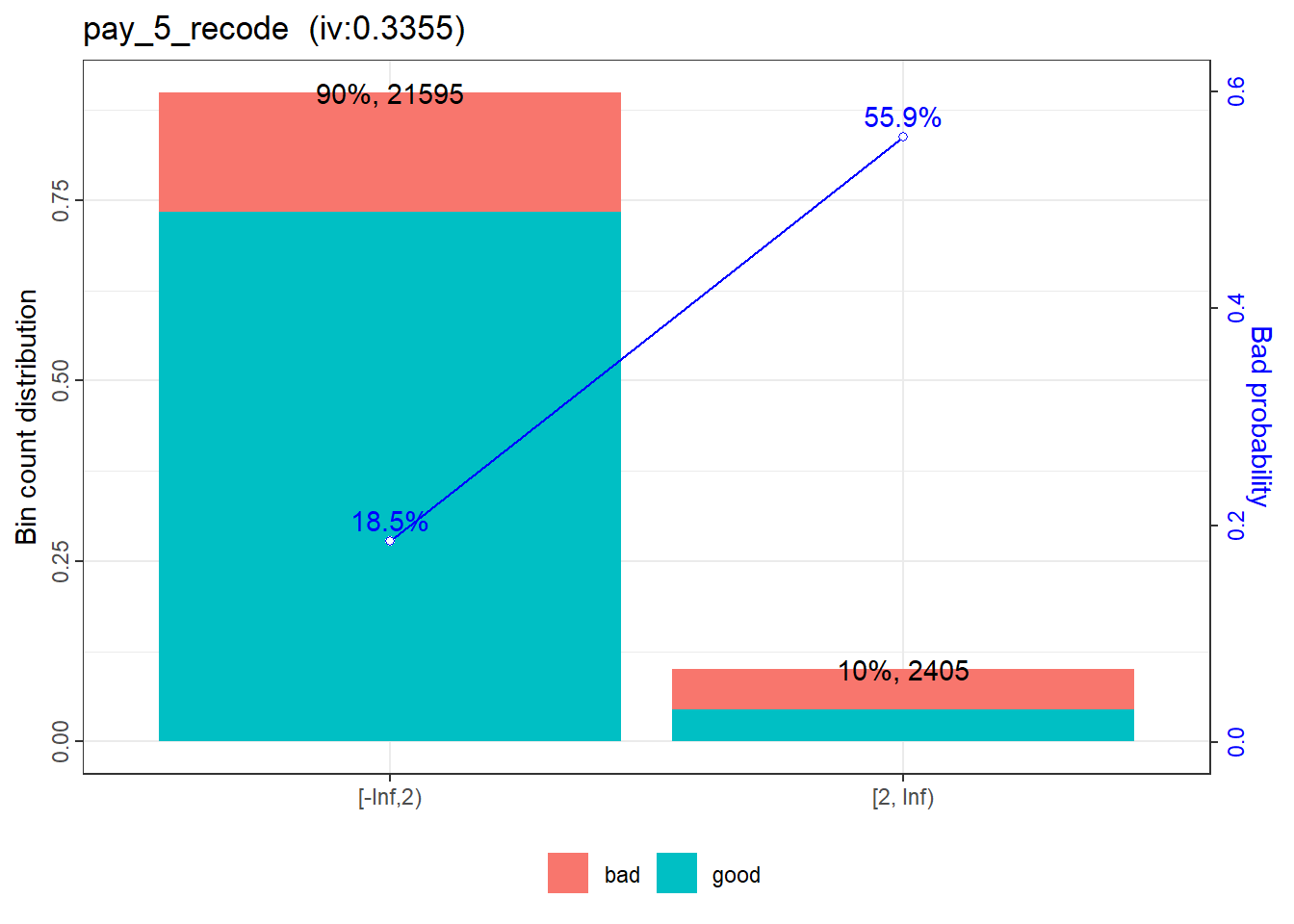
| pay_5_recode | 0.3354879 |
| pay_6_recode | 0.2923127 |
| avg_deq_l3m | 0.8797259 |
| avg_deq_l6m | 0.3011544 |
| max_deq_l3m | 0.7979072 |
| max_deq_l6m | 0.7441613 |
| min_deq_l3m | 0.4711887 |
| min_deq_l6m | 0.0000000 |
| bill_amt1_util | 0.0156583 |
| bill_amt2_util | 0.0133279 |
| bill_amt3_util | 0.0128110 |
| bill_amt4_util | 0.0177728 |
| bill_amt5_util | 0.0182308 |
| bill_amt6_util | 0.0209823 |
| avg_util_l3m | 0.1136387 |
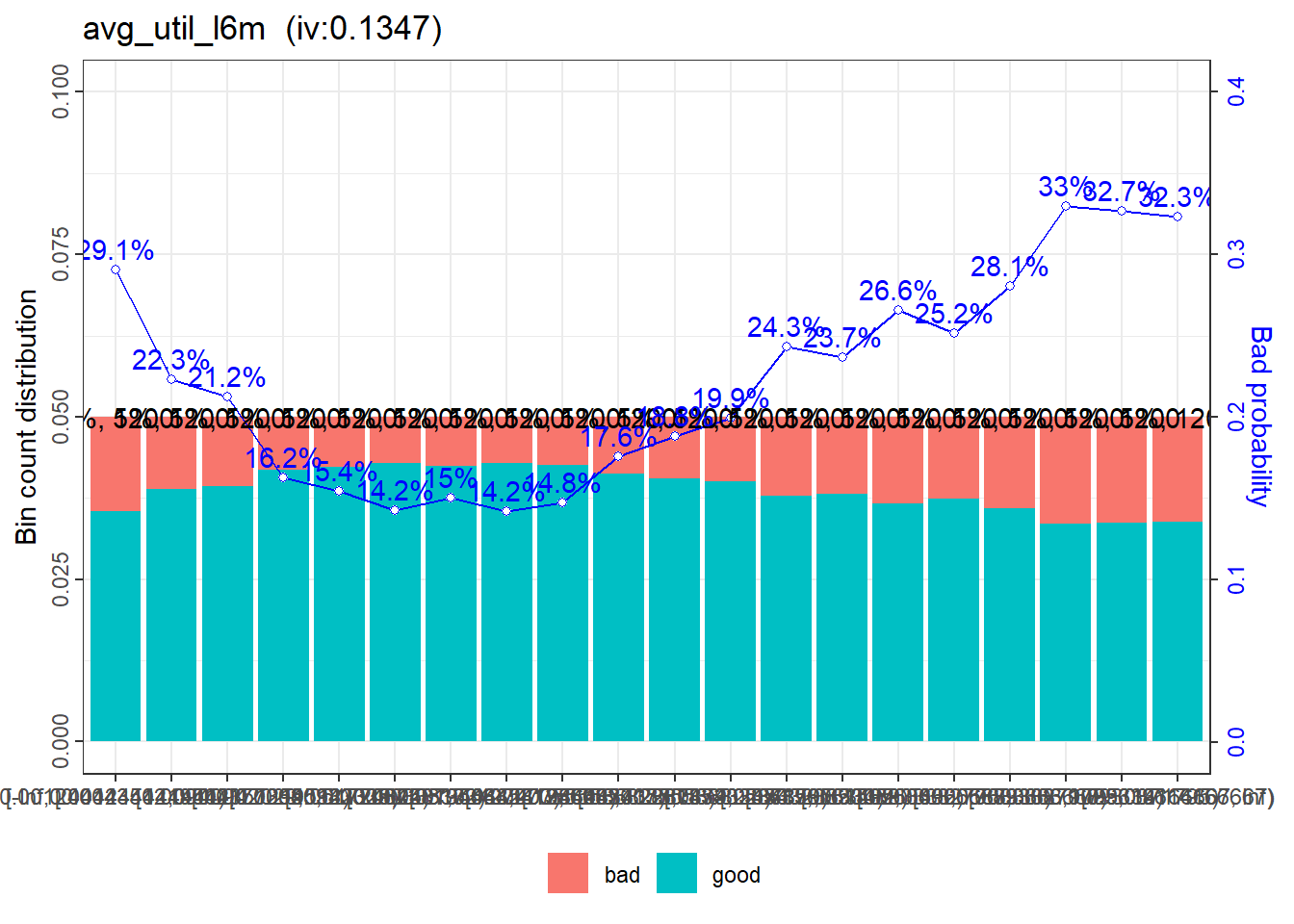
| avg_util_l6m | 0.1346854 |
| max_util_l3m | 0.0899689 |
| max_util_l6m | 0.1039890 |
| min_util_l3m | 0.0146800 |
| min_util_l6m | 0.0072010 |
The reports of the fine classing are contained in fine_class and can be viewed by typing fine_class and running it. Due to the massive amount of reports, only the first one is shown below.
|
|
Note
All of the generated fine classing reports can be saved in csv file using the package erer write.list function. Interested reader is encouraged to explore.
4.2 Initial Variables Removal
As discussed in the section above, new variables are derived because not all raw variables should be used directly. Numeric variables in amount such as balance, limit, payment are not advisable to be used because the variances in their values are large, rendering a credit scorecard unstable. Instead, these variables are converted into ratios (e.g. utilization rates) which are bounded below by zero and the maximum value should not be too far away from 100%.
Also discussed above is variables with a lot of missing values should be discarded. But this does not apply in this post because all variables have no missing values.
Lastly, variables with low predictive power as measured by IV are also removed (IV<0.02). However, since age’s IV is at the boarder line and it is preferable to have some demographic variables in a credit scorecard, age is kept.
With the above, the following variables are removed:
- Low IV
- sex
- education
- marriage
- bill_amt1 to bill_amt5
- pay_amt6
- min_deq_l6m
- bill_amt1_util to bill_amt5_util
- min_util_l3m
- min_util_l6m
- Variables in amount
- limit_bal
- pay_amt1 to pay_amt5
- bill_amt6
|
|
4.2 Variables Clustering
An analyst frequently faces thousands of variables. Even after filtering out variables with high missing values or with low IV values, hundreds of variables will still remain.
In addition to the IV and missing values criteria, variables clustering can be added to the variables reduction tool kit. The idea of variables clustering is to group similar variables into one cluster. Then, a few variables can be selected from each of the different clusters. An additional benefit that stems from variables clustering is that it could help reduce multi-collinearity among variables.
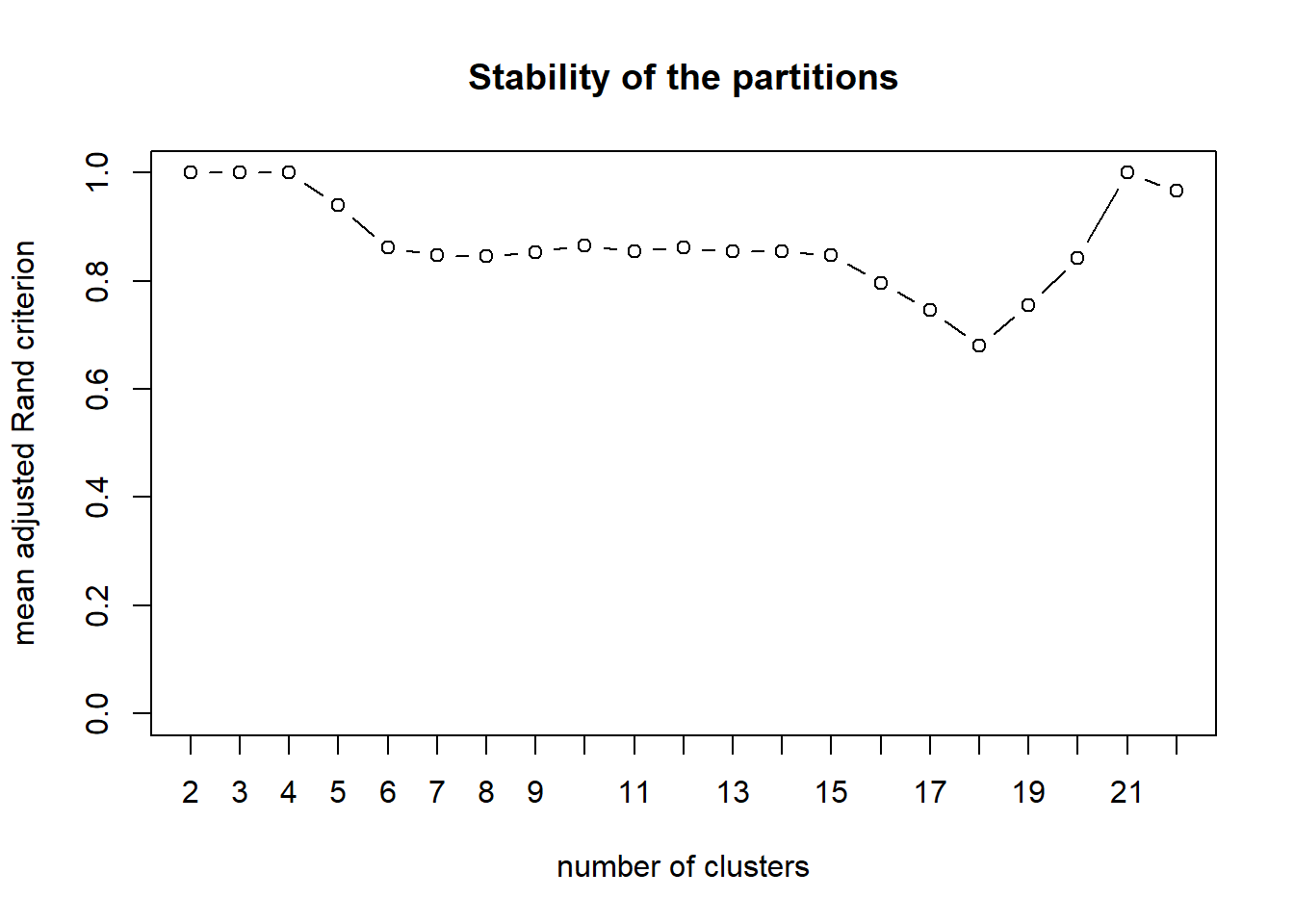
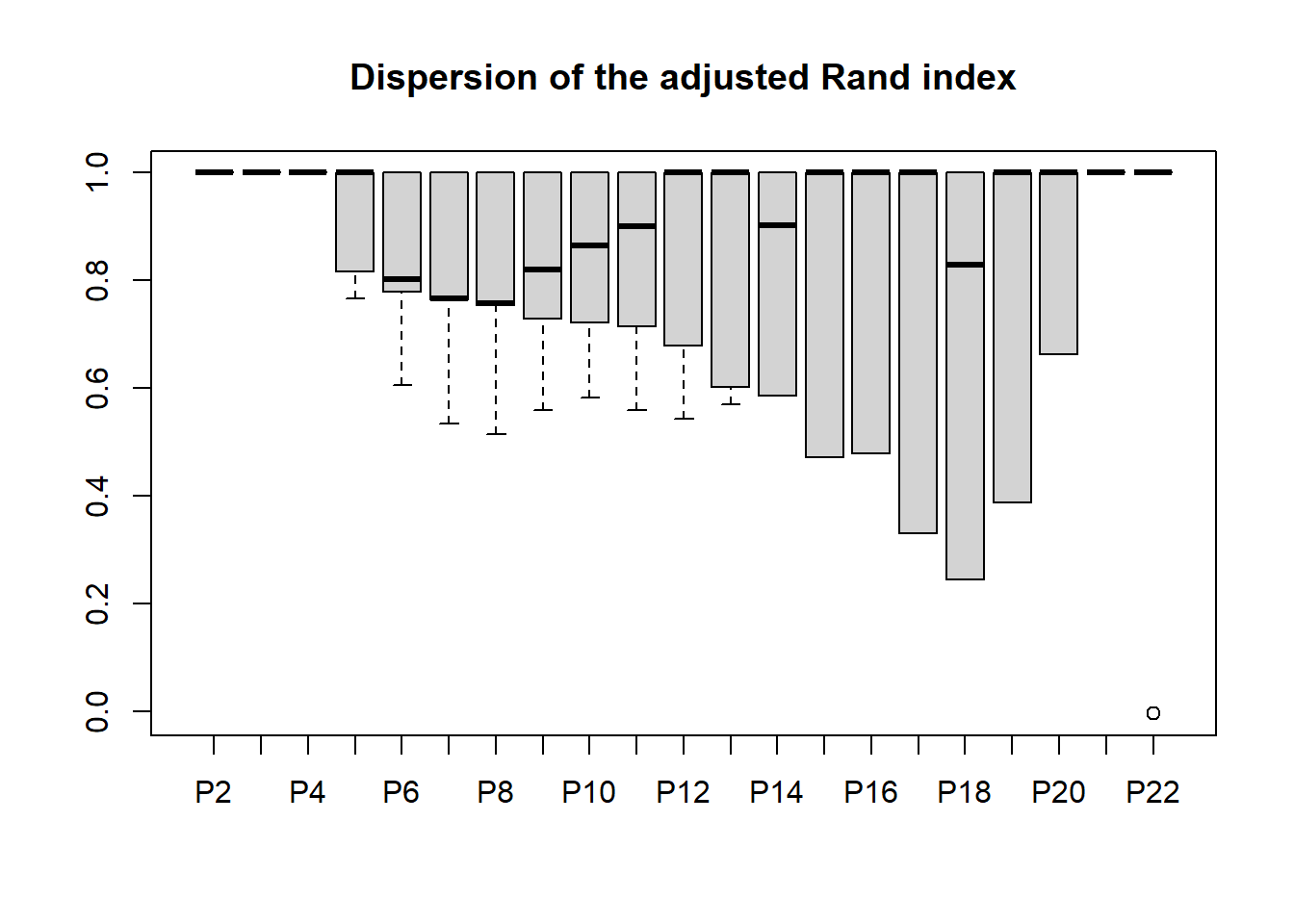
While it is not really applicable in this post as the number of variables is small, variables clustering is conducted for completeness. From the stability plot shown below, 4 clusters appear appropriate for the development sample. Hence, 4 cluster is set using cuttree. In the final output table below, the “x” column is cluster name. The application of this output is provided in the section below.
Note
Variables clustering is computation intensive. It could take up to hours to complete the task if the number of variables is huge.
|
|
|
|
|
|
| x | |
|---|---|
| age | 1 |
| pay_1_recode | 2 |
| pay_2_recode | 2 |
| pay_3_recode | 2 |
| pay_4_recode | 3 |
| pay_5_recode | 3 |
| pay_6_recode | 3 |
| avg_deq_l3m | 2 |
| avg_deq_l6m | 2 |
| max_deq_l3m | 2 |
| max_deq_l6m | 2 |
| min_deq_l3m | 2 |
| min_deq_l6m | 3 |
| bill_amt1_util | 4 |
| bill_amt2_util | 4 |
| bill_amt3_util | 4 |
| bill_amt4_util | 4 |
| bill_amt5_util | 4 |
| bill_amt6_util | 4 |
| avg_util_l3m | 4 |
| avg_util_l6m | 4 |
| max_util_l3m | 4 |
| max_util_l6m | 4 |
4.3 Variables Reduction
One way to utilize the output from variables clustering is combining it with IV as follows:
| var | clus | iv |
|---|---|---|
| age | 1 | 0.0193498 |
| avg_deq_l3m | 2 | 0.8797259 |
| pay_1_recode | 2 | 0.8648336 |
| max_deq_l3m | 2 | 0.7979072 |
| max_deq_l6m | 2 | 0.7441613 |
| pay_2_recode | 2 | 0.5459762 |
| min_deq_l3m | 2 | 0.4711887 |
| pay_3_recode | 2 | 0.4117610 |
| avg_deq_l6m | 2 | 0.3011544 |
| pay_4_recode | 3 | 0.3616306 |
| pay_5_recode | 3 | 0.3354879 |
| pay_6_recode | 3 | 0.2923127 |
| min_deq_l6m | 3 | 0.0000000 |
| avg_util_l6m | 4 | 0.1346854 |
| avg_util_l3m | 4 | 0.1136387 |
| max_util_l6m | 4 | 0.1039890 |
| max_util_l3m | 4 | 0.0899689 |
| bill_amt6_util | 4 | 0.0209823 |
| bill_amt5_util | 4 | 0.0182308 |
| bill_amt4_util | 4 | 0.0177728 |
| bill_amt1_util | 4 | 0.0156583 |
| bill_amt2_util | 4 | 0.0133279 |
| bill_amt3_util | 4 | 0.0128110 |
In cluster 1, there is only one variable. Thus, age is short-listed. In cluster 2, the first 2 variables avg_deq_l3m and pay_1_recode are selected because they have the highest IVs in the cluster. Likewise for cluster 3, pay_4_recode and pay_5_recode are chosen. Finally, in cluster 4, the first 2 variables' IV are quite close and these 2 variables are of average utilization. Therefore, instead of choosing the first 2 variables, the first (avg_util_l6m) and the third (max_util_l6m) are short-listed.
Note
The process presented above is one of many ways of using variables clustering. Different analysts use variables clustering differently.
5.0 Coarse Classing
To do coarse classing, it is necessary to go back to the fine classing reports generated previously, focusing solely on the short-listed variables.
One can use the fine classing reports directly for coarse classing. In this post, plots are used because they are easier for presentation. The plots are shown below one by one for the short-listed variables.
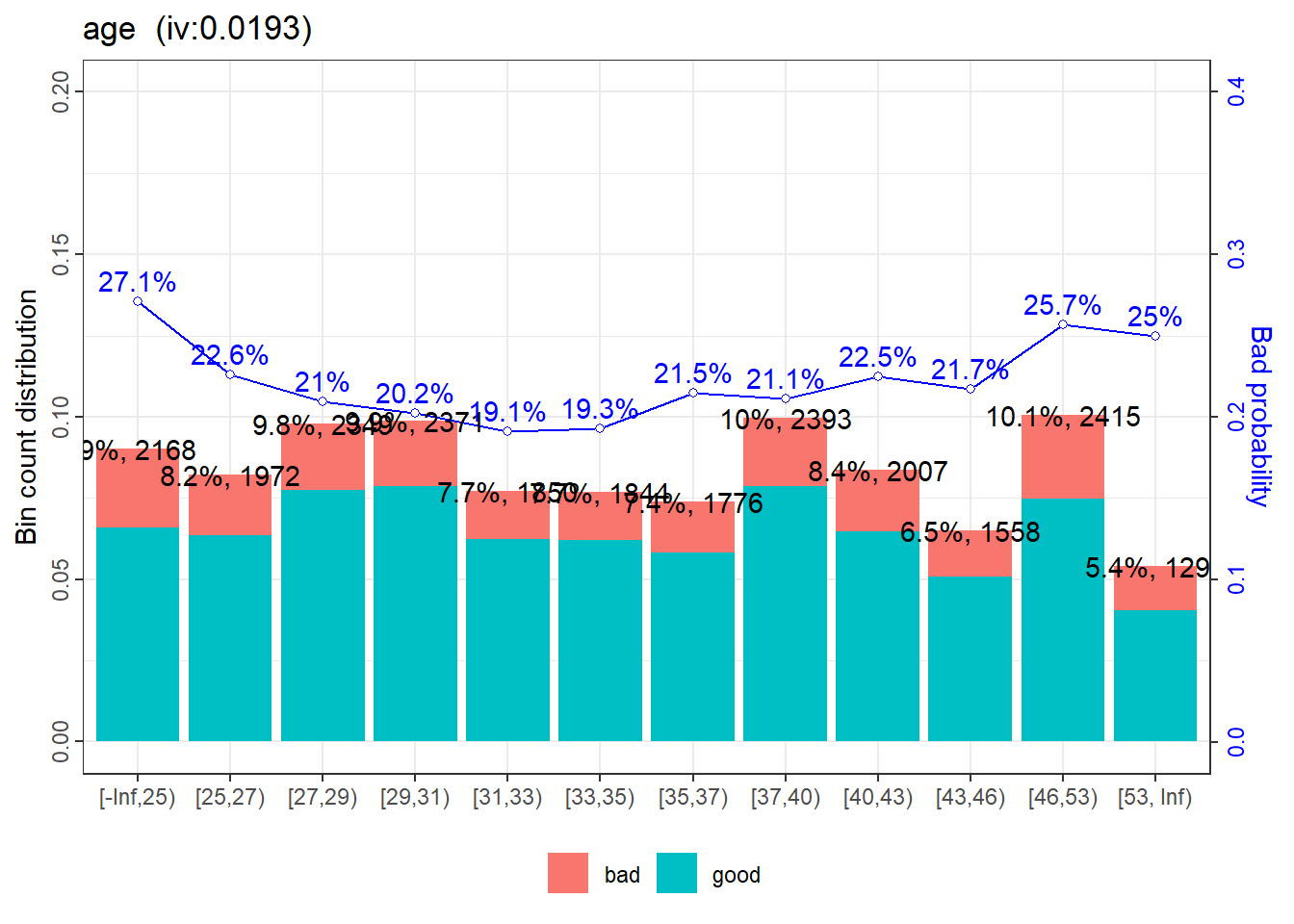
The first plot is for age. Referring to the plot, the bad rates of this variable is of U-shape. A plausible explanation that can be put forward is younger credit card holders are risky because of their lower income. On the other hand, old credit card holders are also risky because of having multiple loans, in retirement, or incurring heavy medical costs etc. For age, the coarse classing could be: a) <25, b)25 to <45, c) 45 and above. Note that the third bin is not starting from 46 as suggested by the plot. 45 is used just to make the bound nicer.
|
|
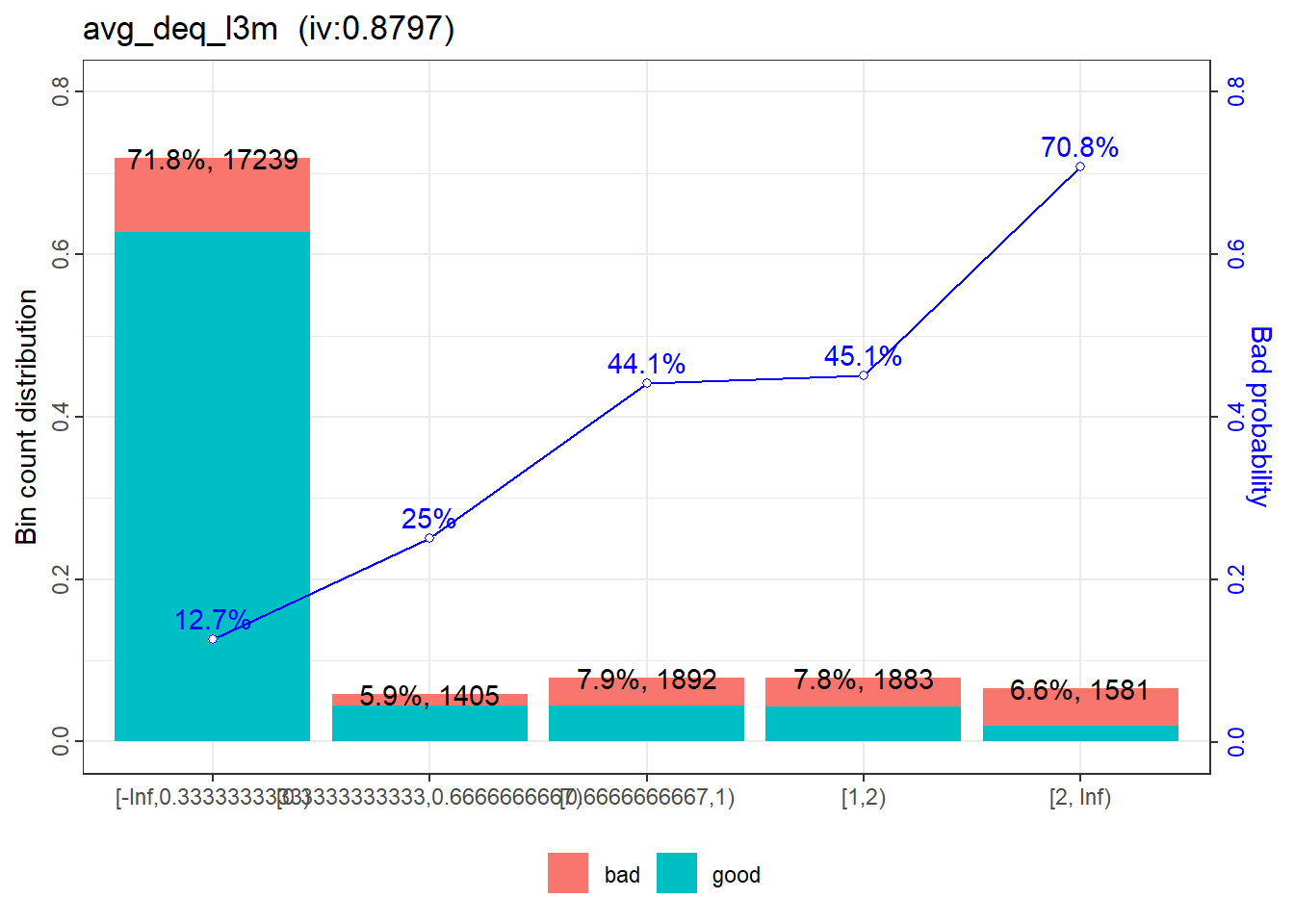
ave_deq_l3m is straight-forward. The bins with 44.1% and 45.1% bad rates are grouped together while others remain unchanged.
|
|
No further classing is necessary for pay_1_recode.
|
|
No further classing is necessary for pay_4_recode.
|
|
No further classing is necessary for pay_5_recode.
|
|
Utilization rates are expected to be monotonic in bad rates. That is, higher utilization rates associate with higher bad rates, or vice versa. Yet, this expectation is not consistent with what shown in the plot of avg_util_l6m. In the plot, it is those with lower utilization rates (i.e. first few bins) have higher bad rates.
For this variable, the coarse classing could be: a) <45%, b) 45% to <83%, and c) 83% and above. Note that minor tweaks are applied to the bounds of the bins. (Refer to the fine class report for the details of the bins.)
|
|
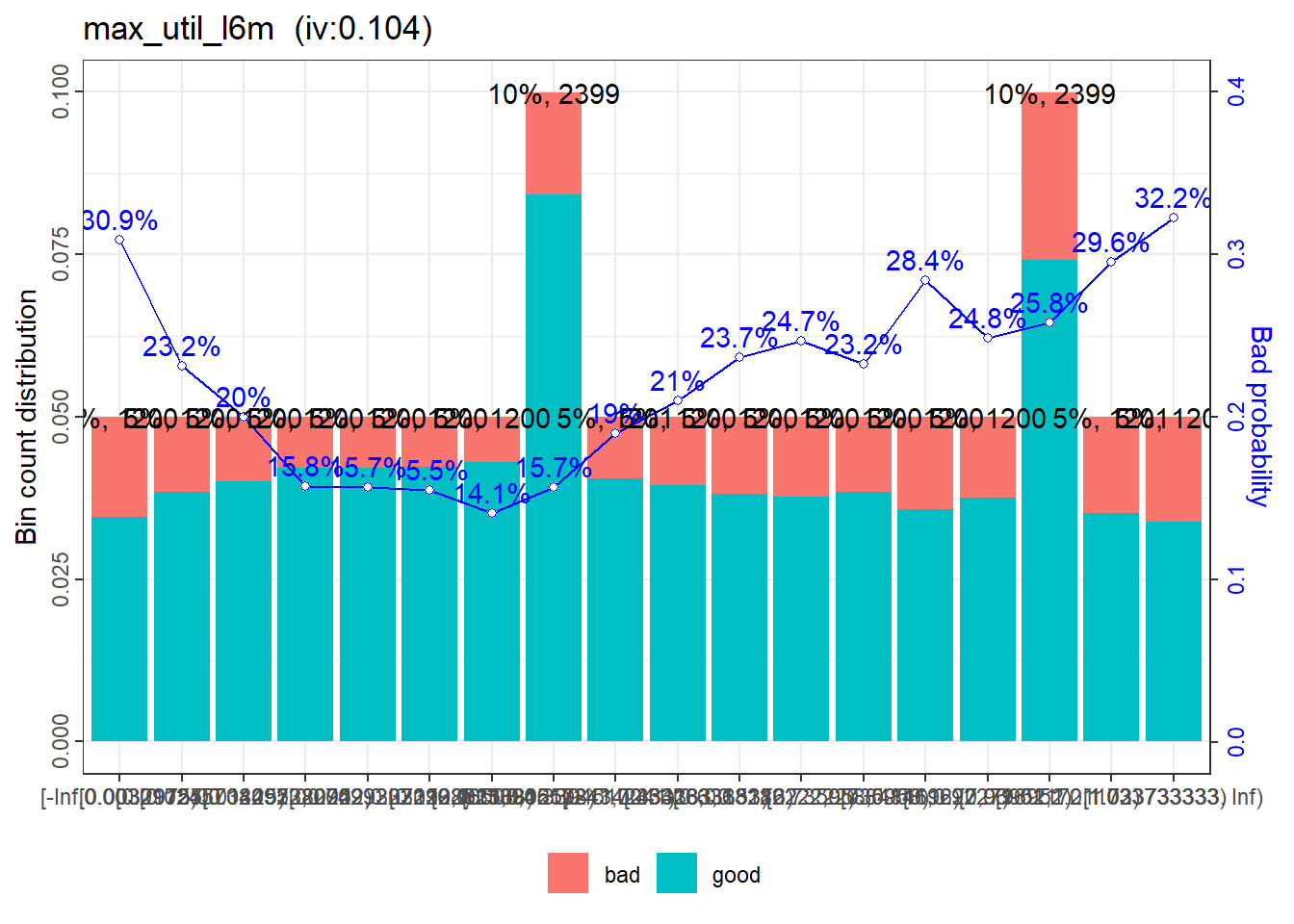
The situation of max_util_l6m is similar to avg_util_l6m. The coarse classing could be: a) <43%, b) 43% to <100%, and c) 100% and above. Minor tweaks are applied to the bounds of the bins.
|
|
The bounds resulted from the coarse classing of all short-listed variables can be saved into a list for future use.
|
|
Danger
What is to be done next is important.
As opposed to other applications, credit scorecards in financial institutions are usually developed to predict “good” instead of “bad” (i.e. default).
The reason of predicting “good” is because credit scores are used as a risk ranking tool. Credit worthy customers (i.e. good customers) are given high scores. And this is easy to communicate to non-technical persons.
Given the afore-mentioned reason, the codes need to be changed slightly. That is, positive = 1 needs to be set as positive = 0. This will not change the IV values and the WOE values of the bins. However, the sign of the WOE values will change. The WOE values with positive = 0 are the values that will be used to develop credit scorecards.
|
|
|
|
|
|
|
|